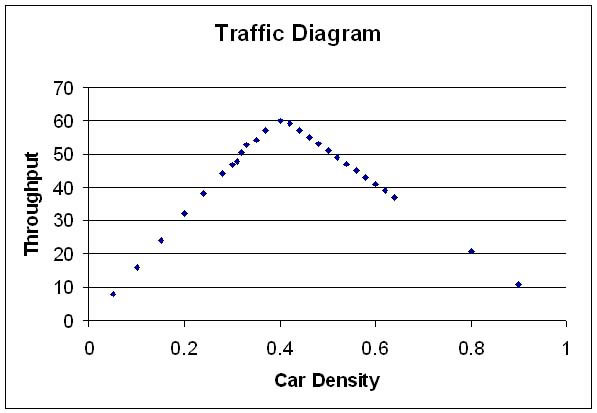
In a simple system, the interaction between autos causes a reduction in the net flow of traffic when the car density increases beyond a critical value-- even when there are no accidents! (Olamide Harrison, '05, thesis)

 

Complexity

Complexity is a field that can appeal to your interest in both pure and applied math, as well as physics. More specifically, the field has a special interest for me because of its connection to one of the areas I teach in our curriculum, statistical physics (Like my colleagues, I find all kinds of physics interesting, in fact, not just the parts I teach). The common thread is that complexity and statistical physics are both concerned with how a large collection of identical elements can produce behavior that is collective.

Collective behavior is characteristic of the whole but not the parts. It is very different from the behavior of the individual component. To illustrate with a example from a study on automobile traffic, a traffic jam is a collective effect that could not be manifested by an individual auto!

Early on, statistical physics showed its power as it explained how behavior, such as the ideal gas law, follows from some simple assumptions about the atoms that make up the gas. Complexity, while it also can be about systems made up of microscopic elements like atoms, extends the search for collective behavior to include macroscopic elements-- like autos, somewhat larger than an atom, you'll agree.

Importantly, complexity theory attempts to encompass systems that are not in equilibrium and, thus, able to display rapid, large scale changes. Examples are effects like avalanches, evolution of species, the behavior of economic systems, and the spread of disease. In each of these cases, and many others, complexity studies are specifically concerned with changes in the collective behavior that occur as time passes. Thus, these are dynamic systems, i.e., time dependent, and may be examined for patterns that show complex, stable, unstable, and chaotic behavior.

Cellular Automata

One way to explore dynamic behavior of large collections of identical elements that interact with each other is through the study of cellular automata, "CA's." Incidentally, there are many java applets on the internet that allow the viewer to observe the behavior of CA's (a search on the phrase "cellular automata" will bring you over 300,000 hits).

The Game of Life

We began our study by looking at the classic "Game of Life." The system consists of a two dimensional square lattice, a chess board if you will, where a square, or cell, is either alive (value of one) or dead (value of zero), or equivalently, occupied or empty. Simple rules are devised that allow you, given a specification of the values of each of the cells on the board at a given moment as either alive or dead, to generate a new chess board where the values of each of the cells are determined. Thus, a second distribution is determined based on the first one and we can follow the time evolution, or mapping, of the pattern of life and death on the board. The starting pattern may grow, shrink, move around the board in an organized way, spawn colonies, etc. The patterns that occur and how the particular rules may affect the patterns and their dynamics allows for seemingly endless and fascinating study. Here is an interesting website to introduce you to the game of life and complexity including an applet that allows you to play the game yourself.

Olamide Harrison (’05),   “On Complexity—An Investigation into Traffic Flow Using Cellular Automata.”

Olamide taking a break from complexity and running in front of the traffic!

That the behavior of traffic may be simulated by a CA and that relatively simple rules for movement of the cars result in complex behavior is illustrated nicely by Nagel and Schreckenberg ( A cellular automaton model for freeway traffic, Journal de Physique I, Volume 2, Issue 12, December 1992, pp.2221-2229). A website explaining the Nagel-Schreckenberg model, including an applet demonstrating CA simulation of traffic flow, is here. The basic phenomena of the traffic jam and the traffic capacity of a road as a function of traffic density emerge clearly from their model. In his study Olamide Harrison, programming the CA using Maple, was able to find these effects also, using only two forward speeds. For example, his traffic flow diagram is at the top of this page.

A popular account of some traffic investigations may be found in the Science News article titled "Stop and Go Science" by Peter Weiss (Science News, 07/03/99. Vol. 156 Issue 1, p8). On campus readers can find it here.

A nonmathematical overview of the field of complexity, intended for the non-specialist (at the back: lots of notes, references, and a bibliography for those wishing to go further) may be found in:

Frontiers of Complexity- The Search for Order in a Chaotic World, Peter Coveney and Roger Highfield (Ballantine Books, New York, 1995).