|
|
 |
Nonlinear dynamics in a mechanical system |
See Peter Millet, James Schreve, and Peter Coxeter, "Phase Space Orbits and the Ping-Pong Ball Impact Oscillator," Phys. Teach. 44, 92-95 (Feb. 2006).
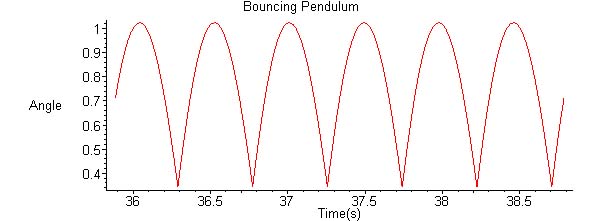
Nonlinear dynamics includes a wide range of physical systems among which are many mechanical examples. These are studied for both their interest as examples of nonlinearity and all that implies, chaos for instance, as well as for practical reasons since many real systems show nonlinear effects. The mechanical system we have been measuring in the lab and modeling on the computer at Hamilton is a form of impact oscillator. We do our modeling using the math software known as Maple. In this apparatus one part, capable of regular oscillatory behavior (think of a pendulum or a spring and mass combination), is given a sharp blow periodically. In such a case, for example, we see a position vs. time behavior that looks like the following (from model calculations):
Phase Space
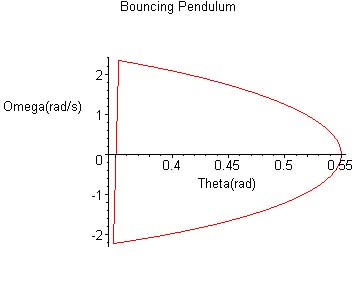
An important tool for the study of motion in nonlinear systems is the phase space plot where we plot velocity versus position (or angular speed versus angle) instead of position versus time. In this kind of plot, a system that repeats its motion after a period of time, say, a pendulum, describes a closed trajectory and occupies a finite portion of phase space. Suppose there are no time dependent forces at work on the system. Then different initial conditions (initial position and initial velocity)-- for the same mechanical system-- may result in different trajectories in phase space. Conversely, identical initial conditions should produce identical trajectories in phase space. Some systems can be extremely sensitive to initial conditions so that, for a very small change in initial conditions there are large changes in the phase space trajectory. That is a characteristic feature of chaotic systems. In general, a study of the shapes or geometry of the trajectories in phase space for a particular system can reveal important characteristics of that system.
| The phase space picture for the bouncing pendulum motion shown above looks like: |
 |
Experiments:
Turning to experimental data, the impact oscillator will show the single bounce pattern seen above and more complicated motions as well, but there is a problem-- the number of data points the motion detector takes in one period is small and we have to do something special to get a clear picture of complex motions. Since the motion repeats itself, we can fold all the position data into one period. To do this we export the data to a spreadsheet program and manipulate it there.
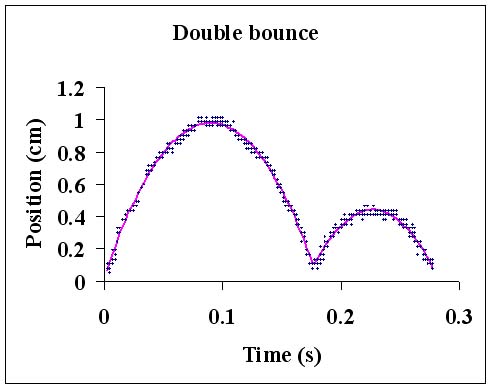
To see the effect of this technique, consider the oscillator operating in a mode we call "double bounce" because of the alternate large and small bounces. First take a look at a few periods of the data without the folding process. The sampling rate provides about 14 data points in the .28 second period after which the motion repeats itself. |
|
Here a ten second run of experimental data is folded into the .28 second period. The curve is fitted using two separate quartics for the two humps. |
 |
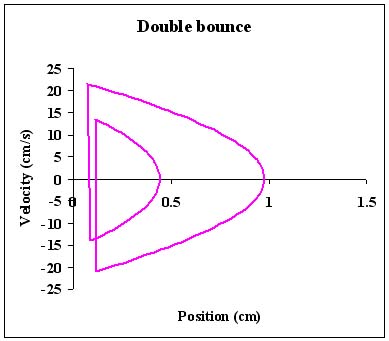
| The phase space diagram calculated from that fit: |
 |
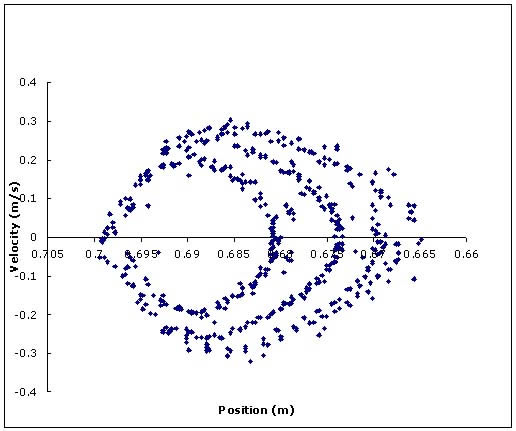 |
It is possible to use the motion detector software to directly produce phase diagrams in "real time." For example, here is such a phase space diagram for ten seconds of data where the system follows an orbit with six loops. |
The velocity calculation produced by the motion detector software averages over a number of points, and cannot help but misrepresent the velocity near the impact since change is so rapid there and the rate at which data is taken is slow. The effect is that the left side of the diagram is rounded instead of having nearly vertical straight segments as in the graph above it. After folding the data into the basic period, as was done for the double bounce motion, it becomes clear that the phase space orbit has six loops. Among the problems we encounter in this study are the need for improvements in precision, noise reduction, control of the non-linearity, accurate modeling of the system, and discovery and characterization of the behavior in phase space in terms of limit cycles, basins of attraction, and chaotic attractors.
Collaboration: This work was done in collaboration with James L. Schreve, Director of Laboratories at Hamilton College and Peter Coxeter ('05).
|
Peter Coxeter (’05), “Further Insights into the Behavior of an Impact Oscillator.”
Peter went on to study aerospace engineering at Washington University. |
|
Todd Johnson ('08),
"Nonlinear Dynamics of the Impact Oscillator and Human Perceptual-Motor Tasks."
Todd is holding the human-operated driver that replaces the mechanical driver in his study of human motor behavior.
|
A closely related thesis on this material:
David Bellows ('03), "Chaos of Mechanical Systems: A Variation of the Bouncing Ball Experiment."
|