Musical Sound

Class 3

Resonance and Normal Modes

NOTE Homework due Friday

Class on Friday in G025

Oscillations

Need

Restoring force, something springy

Moving mass

Sinusoidal motion

Period: time for one complete motion

Frequency=1/Period

Often talk about Angular Frequency ω=2πf

Size of motion called Amplitude

Called Simple Harmonic Motion.

Damping

Friction type force

Force opposes motion causing it

eg. sliding friction, air drag, water drag

Removes energy from system so amplitude falls over time

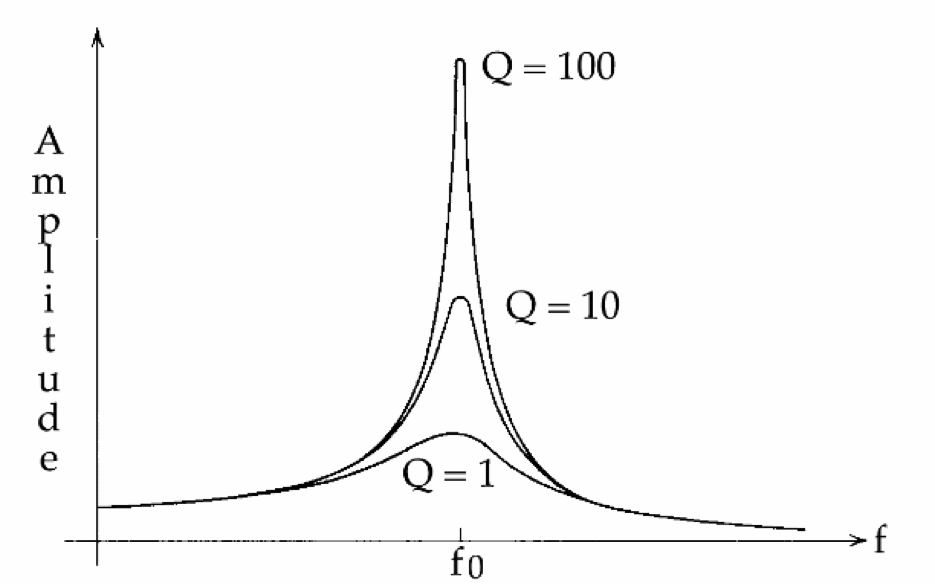
Describe by Q, Quality factor

Q= Energy Stored

Energy Lost in 1 Cycle

For all but lowest Q, ESTIMATE Q=# of cycles before stops

Driven Oscillation

Drive by external periodic force

Drive frequency f (angular ω)

Natural frequency called f₀ (angular ω₀)

For mass on spring ω₀ = √(k/m)

Resonance

If drive frequency far from natural very little happens

If drive frequency near natural get large response

Often call frequency of max. response Resonant Frequency

Resonance Curve

Normal Modes

Normal Mode

A motion in which all parts of the system undergo simple harmonic motion at the same frequency

System with n-masses has n modes for each direction of motion.

Continuous system (eg. string, bar, sheet) will have infinite number of modes. Only the lower ones usually be of interest.

Normally each mode has its own unique resonant frequency (rarely some modes share)

Superposition

Systems with several modes can oscillate in a mixture.

Resulting motion is simple sum of the motions

Called principle of superpostion.

Every possible motion of the system is some mixture of the normal modes.

Superposition Rules

• Every motion of the system can be written as a sum of the normal modes.

• If we analyze the sound spectrum then we shall only find frequencies corresponding to the normal modes.

• The amount of each normal mode depends on the way that the motion was started.

– Modes whose shape is similar to the starting shape will be strongly excited, those with different shapes will be weakly excited.

– When the initial shape is produced by striking or plucking the system then those modes with anti-nodes closest to the striking point will be strongest and those with nodes closest to the striking point will be weakest.

2-D Systems

• System can resonate at any of its normal modes.

• Many resonances at many frequencies

– Lower frequency resonances involve large scale movements of the surface as a whole or only a few sections.

• The displacement it typically large but the velocity low.

• Low modes are widely separated in frequency; factors of 1.5 to 3 are common between the fundamental and the first harmonic.

– Higher frequencies involve smaller scale movements but usually spread over the whole surface.

• The displacements typically grow smaller as the frequency increases.

• The modes tend to get closer and closer together in frequency as the mode number increases.