Homework 1
Your answers are due to be handed in by 5 pm on Wednesday, January 27th.
1) A 2 kg mass on a spring has an equation of motion given by x(t) = 0.9cos(8.0t+0.3) where x is in meters and t is in seconds.
What is a) the amplitude, b) the frequency, c) and the period of the motion.
At t = 1 second, what is d) the displacement, e) the velocity, f) the acceleration, and g) the kinetic energy. Finally, h) find the spring constant k. Whew!
2) Find the equation of motion, x(t), for a 2 kg mass oscillating on a spring with spring constant k = 50 N/m.
At t=1 second, the velocity is +1m/s and the position is 2 m. From the initial conditions you should find two equations with two unknowns which you can solve for A and φ.
3) In some diatomic molecules, the force each atom exerts on the other can be approximated by F=-C/r^2 + D/r^3 where C and D are positive constants. Assume that one atom is at rest and that we are considering the motion of the other atom. Graph the force, F(r) vs. r from r = 0 to r = 2D/C. We only want to see the shape of the curve so the actual constants don’t matter for this problem. Consider the behavior at very small r and at very large r. Which term dominates in each case? Once you determine the basic shape, you should be able to find out where the force is 0 and the position of the minimum.
Use the fact that F = - dU/dr and integration to find the shape of the potential energy curv, U(r)e. Graph this curve. Again, we only care about the shape, especially the position of the minimum.
Show that equilibrium (force = 0) occurs at r = r0 = D/C.
5) Rewrite the following equations in their clearest and most appropriate (sig. figs and all that) forms.
a) x = 3.323±1.4 mm
b) t = 1,234,567±54,321 s
c) λ = 5.33×10-7±3.21×10-9 m
d) r = 0.000,000,538±0.000,000,03 mm
6) The acceleration, a(t), of a particle undergoing SHM is graphed in the figure below.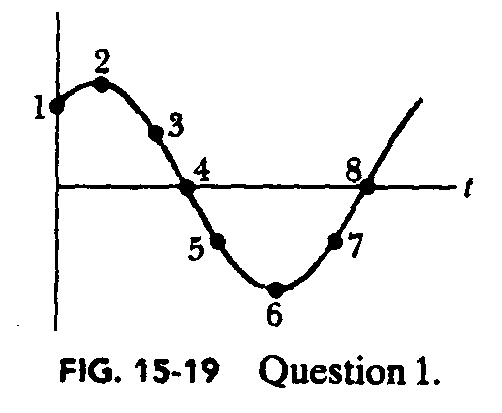
a) Which of the labelled points corresponds to the partcle at -xmax?
b) At point 4, is the velocity of the particle positive, negative, or zero?
c) At point 5 is the particle at -xmax, at +xmax, at 0, between -xmax, or between 0 and +xmax?
In each case explain your reasoning! Do remember that the graph shows acceleration and you are being asked about position and velocity. Hint: do you know how these quantities are realated for SHM?
7) The velocity , v(t), of a particle undergoing SHM is plotted in the figure below.
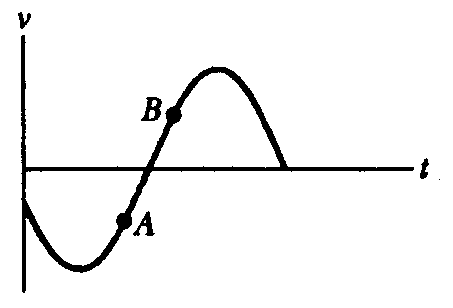
a) At point A, is the particle momentarily stationary, headed toward +
xmax, or headed toward -xmax?
b) At point A, is the particle momentarily stationary, headed toward +
xmax, or headed toward -xmax?
c)Where (at +
xmax, between +xmax and 0, at 0, between 0 and -xmax, or at -xmax) is particle when its velocity is represented by point A?
d)Where (at +
xmax, between +xmax and 0, at 0, between 0 and -xmax, or at -xmax) is particle when its velocity is represented by point B?
e) Is the speed of the particle increasing or decreasing at point A?
f) Is the speed of the particle increasing or decreasing at point B?
8) Use the trigonometric sum of angles formulae (look tham up if you don't yet have them memorised) to find D and φ such that D cos( ωt+φ)=Acos(ωt)+Bsin(ωt). Obviously the answers will be expressed interms of A and B.
9) a) Find the general solution of the differential equation dy/dx = 8x3 - 4x + 1.
b) Determine the particular solution such that y(1)=3.
10) In an experiment performed in the International Space Station, a spherical marble of mass 50g and diameter 1cm is shot into a tank of water at a speed of 1ms-1. Once in the water it experiences a viscous drag force -6πηrv, where r is the radius of the marble, v is is its instananeous speed, and η a numerical constant (the viscosity) which has the value 10-3Pascal-seconds. Draw graphs showing the speed of the marble and the position of the marble as a function of time after it is in the water. Discuss your results.

