Your answers are due to be handed in by 5 pm on Wednesday, February 3rd.
1) A marble thrown into a bowl executes oscillatory motion. Assuming that the inner surface of the bowl is parabolic (y=ax2) and the marble has a mass m, find the angular frequency of oscillation. Neglect friction and assume small oscillation amplitude.
(Hint: Use the gravitational potential energy given by the shape of the bowl to find the force on the marble as a function of horizontal position x. Answer: ω=√(2ag). Note that a has dimensions of inverse length, m-1.)
2) Give an example of a damped oscillation and an example of a resonance. Any example will do, but I would prefer to have one from your personal experience. Obviously you need to tell me why these are good examples.
3) A swing hangs from 2.5 m long ropes. What happens if you push the swing at a frequency of a) 0.2 Hz, b) 0.32 Hz, c) 10 Hz?
4) Most of the ideas of error analysis have important applications in many different fields. The applicability is especially true for the square root rule for counting experiments, as the following example illustrates. The normal average incidence of a certain kind of cancer has been established as 2 cases per 10,000 people per year. The suspicion has been aired that a certain town (population 20,000) suffers a high incidence of this cancer because of a nearby chemical dump. To test this claim, a reporter investigates the town's records for the past four years and finds 20 cases of the cancer. He calculates that the expected number number is 16 (you should show whether this is true!) and concludes that the observed rate is 25% more than expected. Is he justified in claiming that this result proves that the town has a higher than normal rate for this cancer? Again, you must justify your result.
5) Let us say I give you a set of calipers that can measure thickness of a few inches to an uncertainty of ±0.005 inches. If you measure a deck of 52 cards and find that the deck is 0.590 in.then
a) What is the thickness (with uncertainty) of one card?
b) If you want to measure the thickness of a single card to an uncertainty of ±0.00002 in. how many decks of cards should you stack together?
6) a) Assuming that you can measure the length of a simple pendulum to within ±1mm, how long a pendulum would you need to measure g to an accuracy of 0.1%? b) Assuming that you can time a swing to an accuracy of ±0.2 seconds, how many swings should you time to measure to the same accuracy, assuming no error from the length?
7) A 30cm diameter plastic ball with a mass of 400g is suspended from the end of a very light, 5m long fishing line. The viscosity of air (η) is 1.82×10-5Pascal-seconds and air friction obeys Stokes law so that the friction force is F=-6πηrv, where r is radius of the sphere.
a) Write the equation of motion for the system operating as a pendulum. (Hint: because you are trying to find an equation for a pendulum you will need to find a relation between the angular velocity of the ball and its linear velocity, v.)
b) What is the period of the pendulum?
c) How long will it take for the amplitude of pendulum to fall to 63% (that is e-1) of its original value?
d) How many swings will it take before the pendulum is basically stopped?
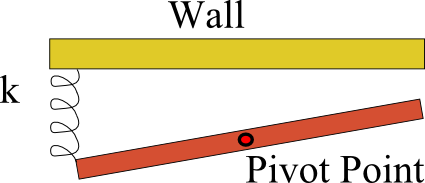
| 8) The figure shows a view from overhead of an apparatus made up from a 1m long uniform rod, mass 0.600 kg, that is freely pivoted about its center. A spring with force constant k=1850 N/m is connected horizontally between one end of the rod and a fixed wall. When the rod is in equilibrium it is parallel to the wall. What is the period of small oscillations that result when the rod is rotated slightly and released? If the amplitude is increased what extra effects will come into play? |  |
9) We saw in class that a damped harmonic oscillator (SHO) driven at its resonant frequency will produce a large, but limited, amplitude response. Examine the case of a an undamped SHO driven at its resonant frequency, ω. Show that you can find a particular solution of the form Btcos(ωt+φ) and discuss how the response differs from the lightly damped case. A little thought will show that this solution is, in the long term, impossible. What will really happen?
10) The amplitude of a lightly damped harmonic oscillator decreases by 3% during each cycle. What percentage of the mechanical energy is lost in each cycle?