Physics 195 Spring 2010 Homework #6

Due by 5 pm Wednesday March 31^st.
Yes this is after break. Do I think that you should leave it til then? No, I don't. I think that you should get it done and handed in next Wednesday (the 10th) and I will be delighted by any that I get by then. But I am not planning to set another homework over break so if your life would be significantly improved by more time then it is yours.

1) Pick a stringed or wind instrument and go off and do a little research to find out and explain (citations but no math needed) how the design of the instrument is affected by the ideas of the Harmonic Series and of resonance. Note that for some instruments the series part will be easy and the resonance part more interesting and for others resonance won't be all that important but the mechanism of getting a harmonic series will be interesting.
(Wikipedia is fine for this. Books in the library on the physics of musical sound are also good. You can sometimes get good stuff in Groves Dictionary too.)

2) A horizontal rope, mass 1.2kg is fixed in place at both ends (x = 0 and x = 2.0m) and made to oscillate up and down in the fundamental mode at a frequency of 5.0 Hz. At t = 0, the point at x = 1.0m has zero displacement and is moving upward (positive y direction) at 5.0 m∕s .

a) What is the amplitude of the motion at that point?

b) What is the tension n the rope?

c) What is the equation y(x,t) for this rope?

3) A handclap on stage in an amphitheatre sends out sound waves the scatter from the terraces of width w = 0.75m (figure below). There is an echo returned from each step of the terrace so the sound that arrives at the listener’s ear is a series of evenly space, short pulses, one from each step. Assume that the speed of sound is 344ms^-1.

a) Assuming that all the paths are essentially horizontal, find the frequency of the string of pulses that return (number of pulses per second).

b) If the width w of the terraces were reduced would the frequency be higher or lower?

4) The speed of sound varies with temperature according to the relationship v_T = 344 + 0.6(T - 20^∘)m∕s where the temperature, T, is in degrees Celcius. An organ pipe is cut so that when the room temperature is 23^∘C the pipe sounds concert A, f = 440Hz. What frequency will the pipe produce on a chilly winter’s day when the temperature in the church is only 8^∘C?

5) Read about the Doppler Effect in chapter 17. A person stands somewhere between two identical, 440 Hz, tuning forks that are both sounding.

a) As the person walks at 3.00 m∕s along the line from one fork to the other the doppler effect alters the frequencies that she hears. What is the beat frequency between the two notes?

b) If, instead of the person walking, she stands still and the two forks move in the same direction at 3.00 m∕s what then is the beat frequency that she observes?

6) A guitar string is plucked at 1/4 of its length from end so that we can take the initial shape of the string to be

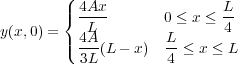
With the help of Maple or otherwise compute the Fourier series for this wave and thus deduce the spectrum of modes that will be observed. Sketch a plot of the Fourier amplitude An as a function of n for the first 10 modes.

7) Consider a Gaussian pulse

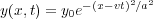
travelling along a string of linear density μ under a tension T.

a) Calculate the kinetic energy associated with the pulse.

b) Calculate the potential energy associated with the pulse.

c) Calculate the momentum carried by the pulse.

Hint: We found the energy densities in class so you will have to integrate over them. The integrals are easiest if we take the string as being infinitely long, -∞≤ x ≤∞. I did them with Maple and strongly recommend that you do the same.

8) When a wave bounces off the fixed end of a wave tray, it does so completely; the returned wave has the same amplitude as the incident wave. Together these can form a standing wave whose nodes are points where the tray does not move at all. When waves bound off a junction (at x = 0) between two wave trays the reflection is incomplete. The returning wave has a smaller amplitude than the incident wave. Consider an incident wave given by y_I(x,t) = Asin(kx - ωt) and a reflected wave given by y_R(x,t) = -ΓAsin(kx + ωt). We would then say that Γ is the reflection coefficient defined by

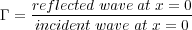
If Γ = 1 then we have the usual condition of complete reflection and get a normal standing wave. If Γ < 1 then the reflection is incomplete and we get a modified standing wave consisting of a travelling piece plus a standing piece..

a) Use trigonometry (Schaum’s!) to add the incident and reflected waves to produce y(x,t) for the incomplete standing wave.

b) Where does the closest maximum to x = 0 occur?

c) Where does the closest minimum occur?

d) Show that the ratio between the amplitude at the maximum and the amplitude at the minimum is given by 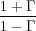, a quantity called the standing wave ratio.

9) Two strings are attached at x = 0. String one has mass per unit length μ₁, and string two has mass per unit length μ₂. An incident wave, Y ₀ = A₀ cos(k₁x - ω₁t), is incident on the boundary from the left. The resulting reflected wave is Y _R = A_R cos(-k₁x - ω₁t) and the transmitted wave is Y _T = A_T cos(k₂x - ω₂t).

a) Briefly describe why ω₂ = ω₁ = ω.

b) Describe the two boundary conditions at x = 0 and use them to find two equations relating A_0,A_R, and A_T.

c) Solve these equations to show that

A_R = 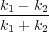A₀ and A_T = 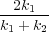A₀.