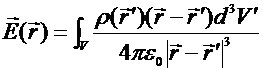Basic Facts Week 9
NOTE: Many of the facts are true ONLY
for the case when the charges creating the electric field are at rest
or very nearly so.
Coulomb's Law: The force F between two
point charges Q1 and Q2 located at positions r1 and r2
respectively is given by
F = Q1 Q2 (r1 - r2)
4πε0 |r1 - r2|3
The force F on a particle with charge q is
caused by an electric field E and is given by
F = q E
Principle of Superposition: The electric field at every point
in space is the vector sum of the electric fields from each of the individual
charges.
Field from a single point charge
The electric field E measured at point r due to a point charge Q at position r' is given
by
E = __Q_(r - r')
4πε0 |r - r'|3
The electric field in the interior of a conductor is
zero.
Field lines are a common way to represent vector fields. They obey the rules
1) Lines are everywhere parallel to the field.
2) Lines start and end only on charges.
3) Field lines are more closely spaced in regions of high field and further
apart in regions of low field.
4) Field lines are elastic (stretchy, but don't like it), flexible (bendy,
but don't like it) and repulsive (they repel each other as if they were all
positively charged).
The Electric Potential difference between two points r1
and r2 is defined to be
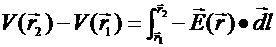
where the integral is along a line joining r1 to r2.
If the E field is caused only by static charges then the value of the integral
does not depend on the path taken and the potential is unique. In that case
we say that the field E is conservative.
In many situations we use an absolute electric potential that is defined by
specifying a unique place at which the potential is set to zero. This is commonly
the point at infinity.
The electric potential at point r arising from a set of
charges Qi at positions ri is given
by
V(r) = ∑i Qi
4πε0|r - ri|
Note that if the charge distribution is continuous then the sum will become
an integral over the volume containing the charge.
The electric potential around a point charge of magnitude Q depends only
on the distance from the charge. Assuming that the potential at infinity is
set to zero then the potential at a point r due to a charge
Q at point r' is given by
V(r) = Q
4πε0|r - r'|
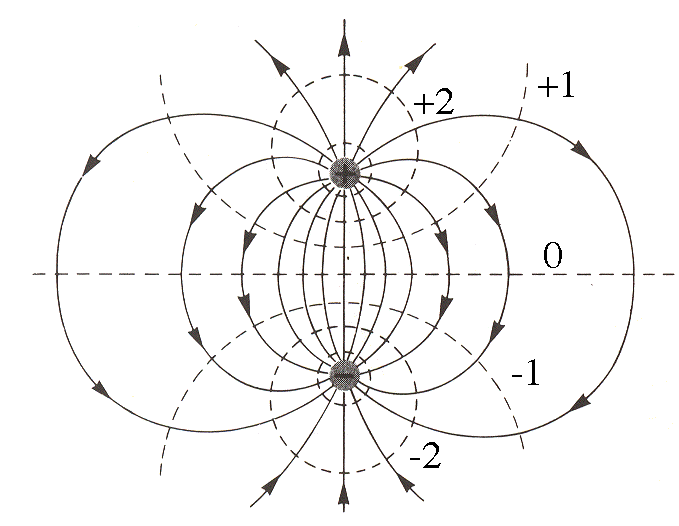
We typically represent the electric potential by drawing lines (in 2-D, surfaces
in 3-D) along which the potential is a constant. These are called Equipotential lines (or surfaces). At every point the equipotentials are perpendicular to
the lines of the electric field and the field points from the higher potential
side to the lower. For example, here are the field and potential around an
electric dipole.
Useful Facts
The field E at a point r caused by
a distributed charge density ρ(r) is given by
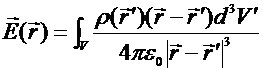
where r' points from the origin to the element of volume dV'
and the integration is over all the space containing the charge.
If the charge is distributed over a plane then replace ρ(r')dV'
by σ(r')da'. Similarly, for a line of charge replace ρ(r')dV'
by λ(r')dV'.