Basic Facts Week 7

Driving Strings

In general bowing or plucking a string produces a spectrum in which the upper harmonics fall in intensity at the rate of 6dB per octave. That is, every doubling in frequency decreases the amplitude of the mode by a factor of 2 and its energy by a factor of 4.

When a string is plucked at a distance L/x from one end there is an additional decrease in the amplitudes of those modes with numbers near n*x where n is some integer (NOT necessarily the mode number!).

When the string is bowed there is very little dependance of the mode structure on bowing point. The shape of the string is fairly independent of the bowing point and the main effect is on the volume of the sound.

The baisc mechanism is stick-slip in which the bow drags the string along until the bowing force and friction is too weak to pull the string any further. At that point the striping starts to slip past the bow and snaps back very quickly until it reaches a position on the other side of equilibrium where the side-to-side speed is low enough that the string sticks to the bow again and the process repeates.

Resonance

When a mechanical system is driven by a periodic disturbance it may exhibit the phenomenon of resonance. If the driving frequency is near to one of the natural mode frequencies of the system then large amplitude oscillations may result.

The details of the resonant behavior depend on the amount of friction in the system. If the system exhibits very little friction then there is very little energy lost in each cycle of oscillation. We quantify this by the Q factor defined as

A system with very little friction is said to have a high Q and a system with a lot of friction to have a low Q.

The size of a resonant system's response depends on the Q of the system and on how close the driving frequency is to the natural frequency of the system. The figure below summarizes the responses of various systems to various drives.

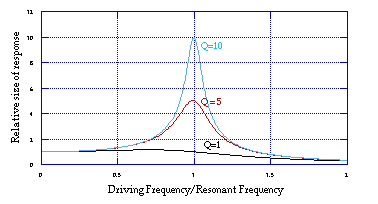
A high Q system will produce a very large response but only to a very narrow range of frequencies right around the natural frequency. A low Q system will produce a less extreme resopnse but will respond to a much broader range of frequencies.

Instrument bodies must provide resonances to support the sound of the instrument without large changes in volume as the pitch changes. This requires moderate Q resonances.

Useful Facts