Basic Facts Week 4

We measure the strength of a sound by its intensity. The intensity is the sound energy crossing unit area in 1 second. It is measured in units of W/m².The intensity of a sound is proportional to the square of its amplitude.

It is convenient to express sound intensities in terms of multiples of the softest sound that can be heard (about 10^-12Wm^-2). These ratios get so large that we express them on a logarithmic scale measured in decibels.The Sound Intensity Level (SIL) corresponding to an intensity I is

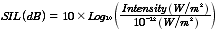
where the log is taken to the base 10.

Similarly, we compare the strengths of two sounds by finding the ratio of their intensities and expressing the answer in decibels.

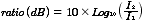
The ear responds non-linearly to sound intensity. It is much more sensitive to changes in sound level at low levels of sound than at high levels. On average a ten fold increase in the intensity of a sound makes the sound twice as loud. The ear is much less sensitive to low frequencies than to high frequencies and the effect is particularly pronounced for quiet sounds.

Aural Perception

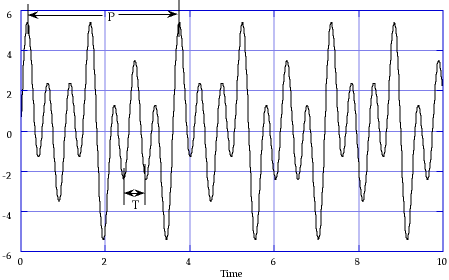
Pitch. In order for a sound to have a clearly defined pitch the waveform must be periodic. The frequency of the sound is perceived as 1/period. In the figure below the ear hears the sound as having the pitch 1/P not 1/T or any other sub period.

Fourier's Theory states that any periodic wave of period P may be built from a set of sine waves whose frequencies form a harmonic series with fundamental frequency f0 = 1/P. Each sine wave must be chosen with exactly the right frequency and phase and the theory provides a mathematical way to find the correct values from the shape of the complex wave.

The individual frequencies that constitute a complex sound are called partials. A periodic sound consists of partials that are members of an Harmonic Series, as set of frequencies with the relationships

f₀, 2f₀, 3f₀, 4f₀, 5f₀, 6f₀, 7f₀, 8f₀, etc.

We call building a complex wave from a set of sine waves Fourier Synthesis and the reverse process is called Fourier Analysis. We call a plot of the Fourier Analysis of a complex wave the Spectrum of the wave.

The timbre of a note is the distinctive color of the sound. It depends in large part on the spectrum of the waveform. The more high frequency components the spectrum has the brighter or tinnier the sound is. Dull sounds have spectra with few high frequency components. The timbre is also affected by the envelope of the sound, the pattern of loudness as a function of time, and by the way that the spectrum changes during the note.

Useful Facts

Here is a table of some common ratios and their equivalents in dB

Decibel Ratios

Ratio	dB
I1 = I2/10	-10dB
I1 = I2/2	-3B
I1 = I2	0dB
I1 = 2×I2	+3dB
I1 = 4×I2	+6dB
I1 = 10×I2	+10dB
I1 = 20×I2	+13dB
I1 = 100×I2	+20dB