Basic Facts Week 5

Two sounds of different pitches form an interval. Ears, at least those of people accustomed to western musical styles, perceive two intervals to be the same if the frequency ratios are the same. That is, a western ear will hear sounds of 200Hz and 300Hz as forming the same musical interval as sounds of 240Hz and 360Hz because 300/200 = 360/240.

Western music is largely based on the intervals of the harmonic series. This is the sequence of pitches that you obtain by multiplying a single frequency by successive integers. Thus we have a harmonic series based on the standard pitch of 440Hz.

Ratio	1	2	3	4	5	6	7	8
Harmonic	1st	2nd	3rd	4th	5th	6th	7th	8th
Interval	Unison	Octave	12th or 1 octave +a fifth	15th or 2 octaves	17th or 2 octaves +a third	19th or 2 octaves +a fifth	-	three octaves
Frequency	440	880	1320	1760	2200	2640	3080	3520

Note: I expect that you all know the ratios for an octave (2:1) and a fifth (3:2). I would not memorize any others but DO memorize the intervals in the table above. Then you can figure out the thirds and the fourth any time you need them.

In antiquity, the western musical scale was constructed based on some of these ratios.
The most fundamental interval is the octave, corresponding to doubling or halving the frequency. Two pitches that are one octave apart sound so similar that we give the notes the same name.
The next most important ratio is the fifth, corresponding to a ration of 3:2, found between the second and third members of the harmonic series.
Closely related is the fourth, a ratio of 3:4, found between the third and fourth members.

The Pythagorean Just scale is constructed using the circle of fifths so that all intervals of a fifth (and thus also a fourth) are in tune but many of the thirds are badly mistuned. The circle does not close because (3/2)¹² is not a power of two.

The modern equally tempered scale is constructed from approximate ratios that allow the division of the octave into 12 exactly equal intervals. We call the interval between adjacent pitches 1 semitone and it corresponds to a ratio of 2^1/12 = 1.05946. We arrange these semitones in a regular pattern called a scale and give them alphabetic names according to an historical scheme. We start from the convention that 440Hz will be called pitch A and then work our way through the alphabet in the following scheme

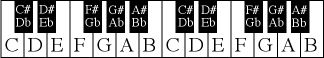
Intervals are usually specified in terms of the number of white notes between two notes. Thus C and G form an interval of a fifth, D and F form an interval of a (minor) third.

Useful Facts

The Pythagorean circle of fifths fails to close by an interval of ratio (3/2)¹²/219, calls the Pythagorean comma. It is about 1/6th of a semitone.

For discussing fine points of tuning the semitone is divided into 100 equal parts called cents. This is a very tiny interval with ratio 1.0005777895.