Resonance

We have seen that any mechanical system can oscillate well only at certain special frequencies, the normal mode frequencies.

If the system is excited at any other frequency then the system will move in a combination of the normal modes. The overall motion will in general be large if the driving frequency is close to a normal mode and small if it is far away.

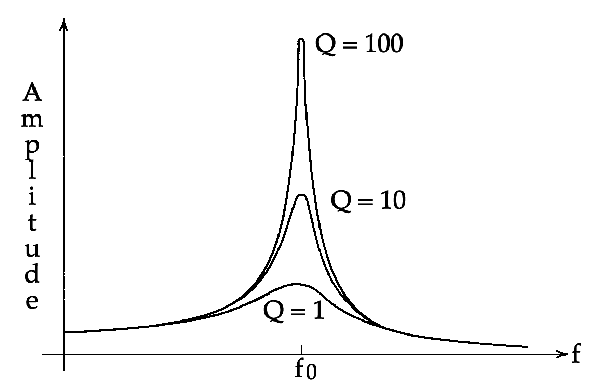
he size of the response and its sharpness in frequency depend upon the friction in the system.

We quantify the friction using the Q (Quality) factor.
Q = Energy Stored in System
Energy lost in 1 Period

If there is very little friction in the system then the Q is high, the system makes a large response to the driving force, and the response is very sharp.

If there is a lot of friction then the Q is low, the response small and broad--extends over wide range of f.

Resonance Curve

Resonance in 2-D Systems

• Many resonances at many frequencies
• Lower frequency resonances involve large scale movements of the surface as a whole or only a few sections.
• The displacement it typically large but the velocity low.
• Low modes are widely separated in frequency; factors of 1.5 to 3 are common between the fundamental and the first harmonic.
• Higher frequencies involve smaller scale movements but usually spread over the whole surface.
• The displacements typically grow smaller as the frequency increases.
• The modes tend to get closer and closer together in frequency as the mode number increases.

Violin Body Resonances

• Need a moderate Q.
• Resonances must be fairly strong to couple sound well to air but
• Resonances must be somewhat broad to avoid sudden changes in volume from note to note.
• Location and width of lowest mode is crucial to a good sound.
• Need lowest mode down near the violins lowest frequency, G3, 196Hz.
• Need that mode to support most of the low notes as the next resonance is not til 400-500Hz.
• Need resonances to extend up above 10kHz even though highest playable note is only 2-3kHz.
• The characteristic violin sound depends on the presence of many upper partials. Those high frequencies must be transmitted to air efficiently for the violin to sound like a violin.
• The upper resonances must not be too different in strength or the violin sound will be too colored by a particular range of frequencies.
• Overall loudness of a note is determined by the response of many body modes to many partials.
• A good violin should not vary in loudness more than about 10dB across the playable range.
• The smoother the response curve is the more even will be tone of the violin.
• Some variation from note to note is desirable as adding individuality to the notes and to the instrument.

Other Bowed Strings

• Other members of the violin family
  • Viola sounds a 5th lower but is only slightly bigger in order to fit under the chin. Weak in its lowest register. Sound is generally darker as highest resonances are weaker than in the smaller violin.
  • Cello sounds 1 octave below the viola. Is a little smaller for its pitch than the violin but not as much as the viola. Size limited by finger range rather than ability to stick it under your chin.
  • Double bass sounds a 6th-8th lower than cello. Quite a bit less than 2x as big so weak in lowest notes. Strings arranged in 4ths to allow for finger range.
• Older family the viols use a slightly different body shape and scale. Strung with gut at lower tension so weaker, thinner sound. Are fretted like a guitar.
• The fiddle is not a different instrument, only a different style of playing. You can play a Stradivarius as a fiddle but the style is designed for cheaper instruments!
• Various non-Western bowed strings including the Rebab that is a prominent member of Javanese Gamelans.

Hutchins Octet

See Carleen Hutchins and Hutchins Consort